Olá, marujos! Hoje explicaremos a lógica proposicional de uma forma descomplicada. A lógica proposicional é a mais famosa lógica simbólica. O assunto é muito complexo e está em íntima ligação com a matemática (inclusive, alguns chamam a lógica proposicional de lógica matemática). Sendo assim, a proposta desse artigo é explicar de forma simples e com vários exemplos o básico da lógica proposicional, aquilo que normalmente é ensinado no Ensino Médio nas aulas de filosofia. Vamos lá!
Lógica Proposicional Descomplicada: Apresentação
Por muito tempo, a única lógica existente era a lógica aristotélica. Conduto, a partir da modernidade, muitos estudiosos começaram a perceber que a lógica clássica não dava conta de interpretar todas as possibilidades do raciocínio, já que ela focava no silogismo.
Foi nesse momento que alguns filósofos e matemáticos buscaram a aproximação da lógica com a matemática. Basicamente, o que eles queriam era poder expressar as proposições e as relações entre as proposições de uma forma simbólica (assim como a matemática trabalha com símbolos). Dessa forma, seria possível verificar a verdade ou falsidade de uma sentença longa sem cometer equívocos devido à interpretação de texto.
A lógica simbólica também é muito útil para exprimir conceitos sem a necessidade de traduzir os termos; evitando-se, assim, ambiguidades contidas nas traduções dos termos de uma língua para outra. Inclusive, com o advento da programação, a lógica simbólica se tornou essencial para o desenvolvimento dos programas de computador.
Lógica Proposicional Descomplicada: Tipos de Proposições e seus Símbolos
Na lógica proposicional, trabalhamos com dois tipos de proposição:
Proposição Simples ou Proposição Atômica: é uma declaração única (eu digo algo sobre algo). Exemplo: Esse carro é preto.
Proposição Composta ou Proposição Molecular: é uma declaração conjunta, que reúne mais de uma declaração única (eu digo vários “algos” sobre vários “algos”). Exemplo: Meu pai é bancário e minha mãe é enfermeira (percebam que aqui existe a união da proposição “meu pai é bancário” com a proposição “minha mãe é enfermeira”).
Para representar simbolicamente uma proposição atômica, usamos uma letra minúscula (pode ser qualquer uma, mas existe uma conveniência de usar “p” ou “q”).
Para representar simbolicamente uma proposição molecular, usamos uma letra maiúscula (pode ser qualquer uma, e não existe uma conveniência nesse caso).
Sendo assim, para o exemplo anterior, teríamos:
meu pai é bancário = p
minha mãe é enfermeira = q
Meu pai é bancário e minha mãe é enfermeira = A
Simbolicamente, seria: A = p . q (daqui a pouco explico esse ponto entre o “p” e o “q”…)
Lógica Proposicional Descomplicada: Tipos de Conectivos e seus Símbolos
Conectivos são as palavras usadas para conectar as proposições. Cada idioma possui um termo específico para representar essas conexões. Sendo assim, aqui eu vou apresentar o nome do conectivo, o conceito desse conectivo, o termo em PORTUGUÊS para esse conectivo e o símbolo usado universalmente para representar esse conceito.
Normalmente, usamos cinco conectivos:
- Negação: serve para apresentar a oposição de uma proposição. Usa o termo “não”, representado por um til “~” (exemplo: “Esse carro é preto”: p / “Esse carro não é preto”: ~ p);
- Conjunção: serve para somar duas proposições. Usa o termo “e”, representado por um ponto “.”. Outros preferem “&” ou “^” (exemplo: “Meu pai é bancário e minha mãe é enfermeira”: p . q);
- Disjunção: serve para apontar uma oposição entre as proposições. Usa o termo “ou”, simbolizado por “v” ou por “w”, porque a disjunção pode ser de dois tipos:
• O “v” indica a disjunção inclusiva, que admite ambas as alternativas (exemplo: “Eu desbloqueio o meu celular com a senha ou com a digital”: p v q);
• O “w” indica a disjunção exclusiva. Nesse caso, trata-se de apenas um ou outro (exemplo: Ele está vivo ou morto: p w q); - Implicação: serve para indicar um enunciado condicional (a ocorrência da primeira condiciona a ocorrência da segunda). Usa o conectivo “se…, então…”, representado por “→”. Outros preferem “⊃” (exemplo: “Se eu estudar, então passarei na matéria”: p → q);
- Equivalência (bicondicionalidade ou bi-implicação): serve para indicar que ambas as proposições condicionam uma a outra (a ocorrência da primeira condiciona a ocorrência da segunda e vice-versa). Usa o conectivo “…se e somente se…”, representado pelo sinal “↔” (exemplo: “Eu poderei sair de casa se e somente se terminar meus afazeres domésticos”: p ↔ q).
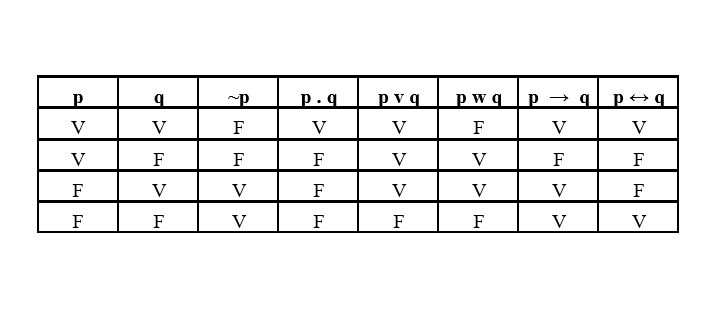
Lógica Proposicional Descomplicada: Tabela-verdade
Como agora utilizamos símbolos para representar as proposições, podemos criar tabelas que demonstram se uma proposição composta é verdadeira ou falsa baseando-se na verdade ou falsidade das proposições simples contidas nela.
A vantagem é que não precisamos parar para interpretar todo o texto da proposição, podendo simplesmente transformar tudo em uma linguagem simbólica e analisar os elementos básicos, que são as proposições simples. Sabendo a verdade ou falsidade de cada proposição, a posição em que ela aparece na sentença e o conectivo que as une, podemos inferir se o conjunto é verdadeiro ou falso.
Negação
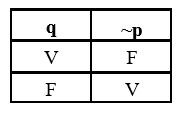
A negação é o único caso em que não existem duas proposições juntas. Conduto, esse é um conectivo importante porque precisamos saber como expressar a negação de uma determinada proposição.
Se p e verdadeiro, então ~p é falso. Se p é falso, então ~p é verdadeiro.
Exemplos:
p: o carro é preto
~p: o carro não é preto
Se o carro é preto, então é falso eu dizer que o carro possui qualquer outra cor. Agora, se o carro não é preto, é verdadeiro eu dizer que o carro não é preto.
Conjunção
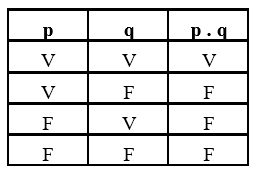
Como a conjunção é uma soma de duas proposições, essa proposição composta só será verdadeira se as duas proposições simples forem verdadeiras. Se qualquer uma das proposições simples for falsa, automaticamente a proposição composta se torna falsa.
Exemplos:
p: o gato é mamífero
q: a cobra é réptil
A = p . q: o gato é mamífero e a cobra é réptil
Nesse caso, a proposição composta é verdadeira porque ambas as proposições simples são verdadeiras.
p: o gato é mamífero
q: o cachorro é réptil
A = p . q: o gato é mamífero e o cachorro é réptil
Nesse caso, a proposição composta é falsa porque a proposição simples “o cachorro é réptil” é falsa.
p: o gato é réptil
q: o cachorro é réptil
A = p . q: o gato é mamífero e o cachorro é réptil
Nesse caso, a proposição composta é falsa porque tanto a proposição simples “o gato é réptil” quanto a proposição simples “o cachorro é réptil” são falsas.
Disjunção Inclusiva
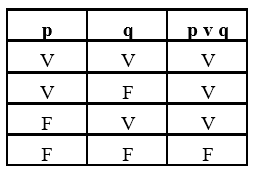
Como a disjunção inclusiva admite qualquer uma das duas alternativas, a proposição composta só será falsa se as duas proposições simples forem falsas. Se uma das proposições simples for verdadeira, automaticamente a proposição composta se torna verdadeira.
Exemplos:
p: eu desbloqueio o meu celular com a senha
q: eu desbloqueio o meu celular com a digital
A = p v q: eu desbloqueio o meu celular com a senha ou com a digital (repare que a alteração na proposição composta foi apenas estética, para ficar mais “bonita”; porém, se eu quisesse, poderia escrever “eu desbloqueio o meu celular com a senha ou eu desbloqueio o meu celular com a digital”).
Nesse caso, eu precisaria saber as configurações do celular para saber se ele admite ambas as alternativas como forma de desbloqueio.
Se for um celular moderno, a proposição composta é verdadeira porque ambas as proposições simples são verdadeiras.
Se for um celular um pouco antigo, a proposição composta ainda é verdadeira porque mesmo não tendo a função de desbloqueio por digital, já existia o desbloqueio por senha.
Agora, se o celular for MUITO antigo (daqueles modelos tipo “tijolão“), a proposição composta será falsa porque ambas as proposições simples são falsas (não existia bloqueio nem desbloqueio de tela nesses celulares).
Disjunção Exclusiva
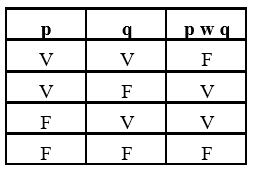
Como a disjunção exclusiva só admite uma das duas alternativas, a proposição composta será verdadeira se uma proposições simples for falsa e a outra verdadeira. Se as duas proposições simples forem ambas verdadeiras ou ambas falsas, automaticamente a proposição composta será falsa.
Exemplos:
p: ele está vivo
q: ele está morto
A = p w q: ele está vivo ou morto (repare que a alteração na proposição composta foi apenas estética, para ficar mais “bonita”; porém, se eu quisesse, poderia escrever “ele está vivo ou ele está morto”).
Nesse caso, conforme aprendemos na biologia, ou alguém está vivo ou alguém está morto. Os casos de mortos-vivos só ocorrem na ficção.
Sendo assim, se a proposição “ele está vivo” for verdadeira e a proposição “ele está morto” for falsa, então a proposição composta é verdadeira (e vice-versa).
Agora, se alguém falar que “ele está vivo” é verdadeiro e “ele está morto” é verdadeiro (ou que ambos são falsos), entraremos em uma contradição lógica (princípio da não-contradição). Sendo assim, a proposição composta é falsa.
Implicação
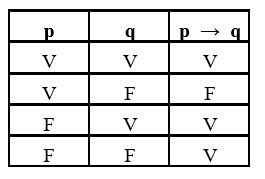
Como a implicação propõe uma condição “Se p, então q“, a proposição composta só será falsa se a primeira proposição simples for verdadeira e a segunda proposição simples for falsa (se é uma condição, a segunda não pode deixar de acontecer se a primeira acontecer). Em todos os outros casos, a proposição composta é verdadeira.
Exemplos:
p: eu estudarei
q: eu passarei na matéria
A = p → q: se eu estudar, então passarei na matéria (repare que a alteração na proposição composta foi estética e ortográfica, para ficar mais “bonita” e para se adequar à norma culta do português; esse é um dos casos em que a língua traz uma limitação ao símbolo).
Nesse caso, eu estou dizendo que o ato de estudar implica necessariamente na condição de passar na matéria. Eu poderia até passar sem estudar, mas não poderia reprovar se eu estudei.
Sendo assim, é verdadeira a proposição composta se as duas proposições simples forem verdadeiras.
Também será verdadeira a proposição composta se as duas proposições simples forem falsas (ou seja, eu não estudei e não passei manteve a lógica da sentença).
Continua sendo verdadeira a proposição composta se eu passar sem estudar (porque eu não coloquei a limitação no ato de passar, mas no ato de estudar).
Agora, se “eu estudar” for verdadeiro e “eu passar na matéria” for falso, eu tenho um problema. Eu coloquei uma condição e essa condição não se concretizou. Logo, eu acabo produzindo uma proposição composta falsa.
Equivalência
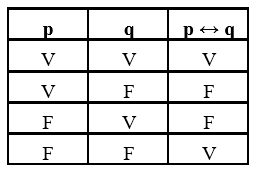
Como a equivalência propõe uma bicondicionalidade (ou seja, ambas as proposições simples afetam uma a outra), a proposição composta será verdadeira se as proposições simples forem ambas verdadeiras ou ambas falsas. Se uma das proposições simples for verdadeira e a outra falsa, a proposição composta será falsa.
Exemplos:
p: eu posso sair de casa
q: eu termino meus afazeres domésticos
A = p ↔ q: eu poderei sair de casa se e somente se terminar meus afazeres domésticos (repare que a alteração na proposição composta foi estética e ortográfica, para ficar mais “bonita” e para se adequar à norma culta do português; esse é um dos casos em que a língua traz uma limitação ao símbolo).
Nesse caso, eu só consigo fazer uma coisa se eu fizer a outra também. Não dá para acontecer uma das proposições simples e não ocorrer a outra.
Sendo assim, é verdadeira a proposição composta se as duas proposições simples forem verdadeiras.
Também será verdadeira a proposição composta se as duas proposições simples forem falsas (ou seja, eu não terminei os afazeres domésticos e não ganhei a autorização para sair de casa manteve a lógica da sentença).
Agora, se eu ganhar a autorização para sair de casa (premissa simples p for verdadeira) e eu não terminar os afazeres domésticos (premissa simples q for falsa), então a proposição composta é falsa (ou seja, não foi mantida a regra da condição). Da mesma forma, se eu terminar os afazeres domésticos (premissa simples q for verdadeira) e eu não ganhar o direito de sair de casa (premissa simples p for falsa), então a proposição composta também é falsa (ou seja, eu não foi mantida a regra da condição).
Lógica Proposicional Descomplicada: Exemplo Prático
Você pode até ter entendido a lógica proposicional, mas ainda deve estar se perguntando onde que se usa isso. Para tentar te ajudar a “visualizar” a aplicação desse conteúdo, imagine um jogo de luta (tipo Street Fighter ou Mortal Kombat).
No jogo, são diferentes personagens e animações de ataque. Entretanto, muitos utilizam a mesma combinação de comandos para dar um golpe especial. O programador, em vez de escrever um comando para cada personagem, escreve uma fórmula lógica simbólica padrão. A mesma coisa ocorre com as partidas: são dezenas de combinações possíveis de partida, e não dá pra escrever todas elas. Tendo a fórmula é só aplicar a cada personagem ou partida.
a) Negação: apertar “pulo” pra pular. O padrão do personagem é no chão. Quando você aperta o botão de pulo, você cria uma negação no padrão e ele sai do chão.
b) Conjunção: especial é “A e B” = são necessários os dois botões juntos para o especial, não tem como soltar ele se os dois botões não forem apertados juntos.
c) Disjunção Inclusiva: especial é C (frente) e [A ou B] = além do C, tanto faz A ou B. Qualquer um dos dois vai garantir o especial.
d) Disjunção Exclusiva: Ou você chuta ou Soca (A ou B) = o personagem só dá um golpe por vez, ou chute ou soco. Se apertar os dois ao mesmo tempo, não acontece nada e se não apertar nenhum também não acontece nada. Tem que ser pressionado um botão ou outro.
e) Implicação: se o golpe acerta o oponente, então tira vida dele = A vida diminui se o personagem levar o golpe (mas não exclui outras formas de perder vida, por exemplo defender um super especial).
f) Equivalência: cada partida só acaba se e somente se um personagem ganhar duas rodadas (dois rounds) = O fim da partida depende completamente de alguém ganhar duas rodadas (rounds), enquanto isso não acontecer, não acaba a partida.
Lógica Proposicional Descomplicada: Conclusão
Espero que esse conteúdo, que não é tão simples quanto parece, tenha ficado o mais claro possível para vocês. Semelhante à matemática, somente com a prática de exercícios é que ele se torna natural e, em certo sentido, automático. A imagem principal desse artigo será uma tabela-verdade com todas as possibilidades utilizando-se duas proposições. Caso a sentença possua três ou mais proposições, é necessário resolver primeiro duas proposições, para depois pegar esse resultado e resolver com a terceira proposição e assim sucessivamente. Na forma simbólica, assim como na matemática, usamos os parênteses ( ), colchetes [ ] e chaves { } para agrupar as proposições que devem ser resolvidas primeiro.
E aí? restou alguma dúvida? Deixa ela aí embaixo, nos comentários. Conseguiu entender tudo? Compartilha esse artigo e ajuda outras pessoas. Quer sugerir algum tema de artigo? Entra em contato comigo.
Até a próxima e tenham uma boa viagem!
———————————————————————————————
Lógica Proposicional Descomplicada: Referências
GALLO, Sílvio. Filosofia: experiência do pensamento. Volume único. 2. ed. São Paulo: Scipione, 2016.
MEIER, Celito. Filosofia: por uma inteligência da complexidade. Volume único. 2. ed. Belo Horizonte: PAX Editora e Distribuidora, 2014.
MELANI, Ricardo. Diálogo: primeiros estudos em filosofia. Volume único. 2. ed. São Paulo: Moderna, 2016.