Olá, marujos! Hoje, mostrarei como você pode estar ensinando a teoria do conhecimento de Hume através do jogo de dados Farkle. Nesse jogo, você irá rolar dados para tentar chegar a grandes pontuações, mas quanto mais ambicioso for, mas risco tem de perder tudo. O aluno, através do jogo, entenderá a crítica à causalidade feita pelo filósofo. Esse é um jogo simples e de baixo custo. Vamos lá!
Relembrando o Conceito
David Hume era um empirista moderno o qual ficou famoso, na sua teoria do conhecimento, por mostrar como as impressões são mais “fortes” que as ideias e como a relação de causa e efeito é falsa.
Segundo o filósofo, impressões são aquilo que vivemos no momento. Por exemplo, quando chutamos uma pedra, a dor na hora do chute é a impressão. Já a ideia é uma lembrança de uma impressão vivida. No exemplo dado, é a lembrança da dor ao chutar a pedra. O filósofo dirá, então, que uma ideia nunca terá o mesmo peso de uma impressão porque, quando recordamos de alguma coisa vivida, essa recordação pode ser mais ou menos intensa (mantendo o exemplo, ao lembrar do chute, podemos achar que foi mais ou menos dolorido do que realmente foi).
Depois, o filósofo continuará demonstrando que cada impressão é única e impossível de se repetir. Já as ideias (lembranças de impressões), por serem uma produção mental, podem se relacionar de diversas formas: por proximidade (que ele chama de contiguidade), por semelhança e pela relação de causa e efeito.
A ciência se vale da relação de causa e efeito (causalidade) para fazer suas predições. Porém, segundo Hume, isso é um problema porque não existem garantias que sempre que ocorra um evento A, se sucederá o evento B. Mesmo que isso tenha se repetido 99 vezes seguidas, não existe certeza que ocorrerá uma centésima vez. Esse pensamento não passa de uma crença pelo hábito.
Dessa forma, a ciência não é uma certeza absoluta, mas uma probabilidade. A certeza de um efeito só se dará quando ele de fato ocorrer (impressão).
Para aprender com mais detalhes esses conceitos e com muitos outros exemplos, recomendo a leitura do texto: Empirismo de David Hume Descomplicado.
Ensinando a Teoria do Conhecimento de Hume através de Jogo: Farkle
Apresentação
O jogo Farkle é um jogo de dados antigo. Não se tem certeza de sua origem, sendo a versão mais aceita que o jogo “chegou” (não se sabe de onde nem como) nos navios franceses por volta de 1600 e foi sendo passado de geração em geração.
Nesse jogo, usamos seis dados de seis faces. A combinação de dados iguais ou sequenciais geram pontos. Pode-se arriscar jogar mais dados e acumular mais pontos ou ser conservador, jogando os dados menos vezes e pegando menos pontos. Quem atingir a maior pontuação após um valor pré-estabelecido ser batido, ganha.
Material
Precisamos apenas de seis dados de seis faces para o jogo. Se quiser, um copo para sacudir os dados (apesar de que podemos fazer isso na mão) e um tabuleiro ou bandeja (apesar de que podemos jogar no chão ou sobre a mesa mesmo).
Também será necessário papel e caneta / lápis para anotar as pontuações de cada jogador (na sala de aula, pode-se usar o quadro negro e caneta de quadro / giz).
Regras do Jogo
O jogo é individual e não tem limite de jogadores.
Escolhe-se um jogador para começar e depois segue a passagem dos dados no sentido horário. Pela regra “oficial”, a escolha de quem começa é feita pelo lançamento de todos os dados por cada jogador. O que tirar a soma mais alta começa.
A cada rodada, o jogador começa lançando todos os seis dados para tentar uma pontuação seguindo a tabela abaixo:
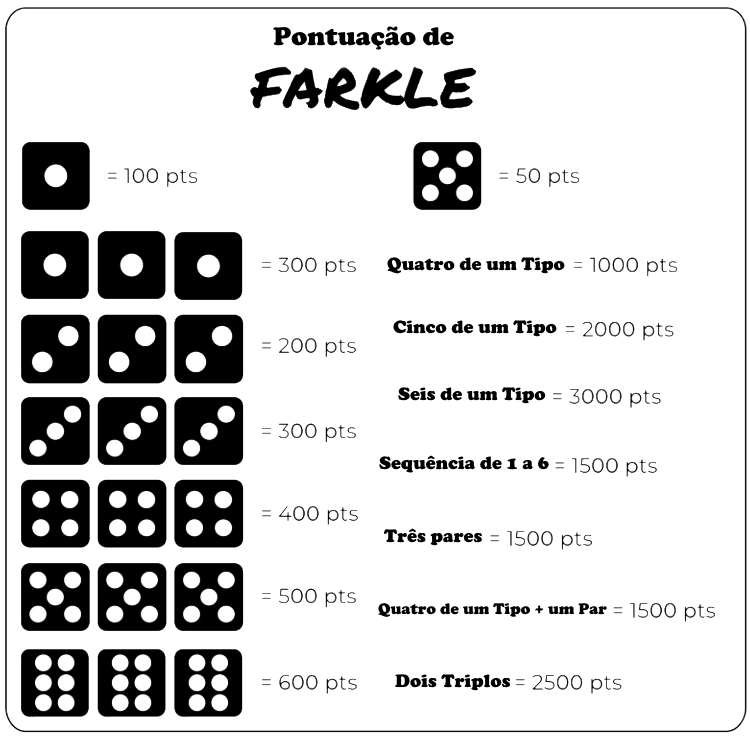
Imagem traduzida do original: https://www.reddit.com/media?url=https%3A%2F%2Fpreview.redd.it%2Fw6ohvsjof6ga1.png%3Fauto%3Dwebp%26s%3Dafa92a7bc5bdc9111c0fe389767ead803187d0ba
Após o primeiro lançamento, ele precisa separar pelo menos um dado e lançar os restantes. Esse(s) dado(s) separado(s) precisa(m) ter uma pontuação.
Os únicos dados que pontuam sozinhos, sem precisar combiná-los com outros, são o 1 e o 5. Sendo que o 1 vale 100 pontos e o 5 vale cinquenta pontos.
No segundo lançamento, os dados lançados precisam pontuar entre eles novamente (não podem ser combinados com aqueles que já foram separados). Separa-se novamente um ou mais dados desse segundo lançamento e lança-se os restantes. E assim se segue.
A rodada do jogador acaba quando ele decide parar após atingir uma pontuação que lhe satisfaça e, assim, guardar os pontos que acumulou ou quando “Farkla”.
“Farklar” é fazer um lançamento de dados que não pontua nada. Se o jogador “farklar”, ele perde todos os pontos que tinha acumulado naquela rodada e passa a vez.
Caso um jogador lance dados de tal forma que, no final dos seus lançamentos, ele conseguiu pontuar com os seis dados, ele ganha o direito de jogá-los novamente e buscar ainda mais pontos (porém, continua correndo o risco de “farklar” nessa nova etapa e perder tudo o que acumulou).
Exemplo de Rodada
Exemplo 1
- Joguei seis dados e tirei 2,2,3,3,3 e 6;
- Eu separo a trica de 3 para juntar 300 pontos e lanço os três dados restantes tirando 1,2,2;
- Eu separo o 1 para juntar 100 pontos e pondero se vale a pena jogar esses dois dados restantes;
- Eu decido parar e guardar 400 pontos.
Exemplo 2
- Joguei seis dados e tirei 2,2,3,3,3 e 6;
- Eu separo a trica de 3 para juntar 300 pontos e lanço os três dados restantes tirando 1,2,2;
- Eu separo o 1 para juntar 100 pontos e pondero se vale a pena jogar esses dois dados restantes;
- Eu lanço os dois dados restantes e não tiro nenhum 1 ou 5 e “farklo”;
- Eu perdi os 400 pontos que tinha juntado e passo a vez para o próximo jogador.
Exemplo 3
- Joguei seis dados e tirei 2,2,3,3,3 e 6;
- Eu separo a trica de 3 para juntar 300 pontos e lanço os três dados restantes tirando 1,2,2;
- Eu separo o 1 para juntar 100 pontos e pondero se vale a pena jogar esses dois dados restantes;
- Eu lanço os dois dados restantes e tiro um 1 e um 5;
- Eu separo esses dados para acumular 150 pontos e ganho o direito de jogar novamente todos os seis dados (se eu quiser);
- Nesse momento, eu tenho acumulado 550 pontos e posso lançar os seis novos dados para pontuar mais ou parar. Se eu continuar, repete-se todo o passo-a-passo da rodada.
Fim de Jogo
Quando um jogador pontuar 10000 pontos ou mais, inicia-se a volta final.
Todos os demais jogadores jogam mais uma vez para tentar bater a pontuação daquele que chegou ao topo. Ou seja, vão para o tudo ou nada.
No final dessa última volta, quem tiver mais pontos ganha.
Ensinando a Teoria do Conhecimento de Hume através de Jogo: Aplicação na Aula
Preparação
Puxe a mesa do professor ou uma mesa dos alunos para o meio da sala e faça com que todos fiquem em volta.
Decida se o jogo será individual ou em grupo. Eu acho que, devido ao número de alunos, seria melhor jogar em grupo (é até interessante porque vai obrigá-los a debater sobre a hora de parar ou continuar). Se for grupo, escolha um líder para ter a palavra final e, assim, evitar perder tempo com impasses.
Coloque o nome dos alunos ou dos grupos no quadro ou papel para marcar a pontuação.
Explique as regras do jogo e comece.
Jogando
As rodadas seguirão as regras normais do jogo, com as decisões tomadas pelo jogador ou grupo e pontuação sendo anotada até termos um vencedor.
Premiação
Pode-se dar pontos de participação para todos e pontuação extra para quem ganhar.
Se existir a possibilidade, pode-se dar alguma guloseima ou experiência diferenciada ao(s) vencedor(es).
Ensinando a Teoria do Conhecimento de Hume através de Jogo: Relacionando o Jogo com a Matéria
A ideia é jogar após a explicação.
Todos os jogos de dados mexem com probabilidade. A chance de sair um dos números em um dado sempre será 1 para 6.
Porém, existe a crença na sorte, de que aquela rodada vai sair o número certo, que se o número não saiu antes vai sair agora ou que se já saiu uma vez vai sair de novo. Essa é a “magia” nesse tipo de jogo, que gera a diversão.
Após a explicação da matéria e ada conclusão do jogo, o professor refletirá sobre o modo como os alunos jogaram. Se eles foram mais racionais e se apegaram às estatísticas ou se eles foram mais emocionais e tentaram a sorte.
O professor pode questionar os alunos se eles pararam para pensar que a causalidade é uma crença, como dizia Hume, e não criaram especulações do tipo “agora vai dar certo” ou se eles ignoraram tudo e foram para o risco incalculado.
Não é para fazer um julgamento de certo ou errado na atitude de cada aluno, mas apenas refletir como funciona a nossa mente, provando que Hume estava certo em dizer como o ser humano cai facilmente na crença da causalidade por causa do hábito.
Ensinando a Teoria do Conhecimento de Hume através de Jogo: Interdisciplinaridade
Esse jogo pode ser feito com o professor de matemática.
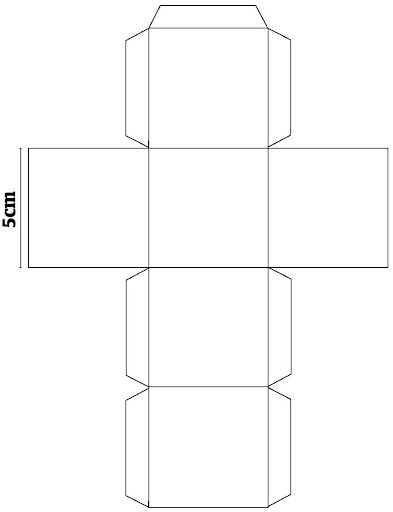
Para essa colaboração, os dados deverão ser criados em papel, nesse modelo em branco “clicável” abaixo:
Com caneta, o professor de matemática irá escrever em cada face do dado um cálculo da matéria que ele está dando cujo resultado seja 1, 2, 3, 4, 5 ou 6 (uma variação como 10, 20, 30, 40, 5o e 60 também seria aceitável).
O desafio extra aqui é que os alunos terão que fazer os cálculos para saber a qual número aquela face do dado corresponde. O ideal é que nunca se repita o mesmo cálculo matemático para não ficar fácil ao ponto de apenas se associar os mesmos cálculos, sem precisar resolvê-los.
Digamos, por exemplo, que o professor está dando logaritmo. Nesse caso, ele colocaria vários logaritmos diferentes para serem calculados cujos resultados seriam esses que falei, correspondendo aos valores dos dados.
Sei que essa variação dará muito mais trabalho e demandará muito mais tempo, mas é uma possibilidade de brincar enquanto se estuda.
Ensinando a Teoria do Conhecimento de Hume através de Jogo: Conclusão
Jogos de dados são sempre legais, divertidos e desafiadores. Esse é um jogo relativamente simples e que consegue trabalhar a proposta filosófica de Hume de um jeito lúdico. Acredito que os alunos irão se divertir bastante ao mesmo tempo que perceberão como é fácil se deixar levar pela emoção e abandonar a razão quando parece que a sorte está do seu lado!
E aí? Alguma parte ficou confusa? Deixa sua dúvida nos comentários! Conhece algum professor de filosofia? Compartilha esse artigo com ele! Quer sugerir outros conteúdos de teoria do conhecimento para receberem uma aula diferenciada? Entra em contato comigo!
Até a próxima e tenham uma boa viagem!
———————————————————————————————
APOIE NOSSAS VIAGENS!
Faça um PIX de APENAS R$0,10 (dez centavos)

Chave PIX: contato@naudosloucos.com.br
———————————————————————————————